[文章目录]
Description
某软件公司正在规划一项n天的软件开发计划,根据开发计划第i天需要ni个软件开发人员,为了提高软件开发人员的效率,公司给软件人员提供了很多的服务,其中一项服务就是要为每个开发人员每天提供一块消毒毛巾,这种消毒毛巾使用一天后必须再做消毒处理后才能使用。消毒方式有两种,A种方式的消毒需要a天时间,B种方式的消毒需要b天(b>a),A种消毒方式的费用为每块毛巾fA, B种消毒方式的费用为每块毛巾fB,而买一块新毛巾的费用为f(新毛巾是已消毒的,当天可以使用);而且f>fA>fB。公司经理正在规划在这n天中,每天买多少块新毛巾、每天送多少块毛巾进行A种消毒和每天送多少块毛巾进行B种消毒。当然,公司经理希望费用最低。你的任务就是:为该软件公司计划每天买多少块毛巾、每天多少块毛巾进行A种消毒和多少毛巾进行B种消毒,使公司在这项n天的软件开发中,提供毛巾服务的总费用最低。1≤f,fA,fB≤60,1≤n≤1000
想了想建图,然后YY对了,啊哈哈哈。
如果前一天买新毛巾留到现在等同于今天买毛巾。
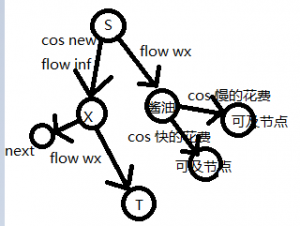
每天用完的毛巾是定值,那么从s再引一条边,限流,然后通过两条有花费的路径到达可及的节点。
1~n建一条链,每个点向汇点连边限流,s向每个点连边,花费为新毛巾的花费,费用流。
图大概这样:
#include <queue>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long ll;
#define inf 0x3f3f3f3f
#define rint register int
int n,s,t,ne,kt,kw,mt,mw,ni[1100];
ll cos;
int head[2100],to[21000],nxt[21000],f[21000],w[21000],cnt=1;
int path[2100];
inline void add(int x,int y,int ff,int ww)
{
to[++cnt]=y; nxt[cnt]=head[x]; head[x]=cnt; f[cnt]=ff; w[cnt]=ww;
to[++cnt]=x; nxt[cnt]=head[y]; head[y]=cnt; f[cnt]=0; w[cnt]=-ww;
}
int dis[2100];
bool v[2100];
queue<int>q;
bool spfa()
{
memset(dis,0x3f,sizeof dis);
while(!q.empty()) q.pop();
memset(v,0,sizeof v);
q.push(s); v[s]=1; dis[s]=0; int i,x,y;
while(!q.empty())
{
x=q.front(); q.pop(); v[x]=0;
for(i=head[x];i;i=nxt[i])
if(f[i]>0&&dis[y=to[i]]>dis[x]+w[i])
{
dis[y]=dis[x]+w[i];
path[y]=i^1;
if(!v[y]) q.push(y),v[y]=1;
}
}
return dis[t]<inf;
}
void mincost()
{
int i,tmp;
while(spfa())
{
tmp=inf;
for(i=t;i!=s;i=to[path[i]]) tmp=min(tmp,f[path[i]^1]);
for(i=t;i!=s;i=to[path[i]])
{
f[path[i]]+=tmp;
f[path[i]^1]-=tmp;
cos+=1ll*w[path[i]^1]*tmp;
}
}
}
int main()
{
scanf("%d%d%d%d%d%d",&n,&kt,&mt,&ne,&kw,&mw);
rint i,j;
for(i=1;i<=n;++i) scanf("%d",ni+i);
s=2*n+1,t=s+1;
for(i=1;i<=n;++i)
{
if(i!=n) add(i,i+1,inf,0);
add(s,i,inf,ne);
add(s,n+i,ni[i],0);
add(i,t,ni[i],0);
if(i+mt+1<=n) add(n+i,i+mt+1,inf,mw);
if(i+kt+1<=n) add(n+i,i+kt+1,inf,kw);
}
mincost();
printf("%lld",cos);
return 0;
}