[文章目录]
Description
现在有一个非常不走运的家伙,他想成为那个玩的最好的人,他现在知道了所有比赛的安排,他想知道,在最好的情况下,他最少只需要赢几场就可以赢得冠军,即他想知道比赛以后赢的最多的那个家伙最少会赢多少场.1 <= n <= 10 000, 0 <= m <= 10 000; n 表示一共有多少个参赛者, m 表示有多少场比赛
当一个答案合法,比它大的答案也一定合法,二分答案。
那么久相当于给你m个点对,每对必须选一个,每个点最多被选x次。所以
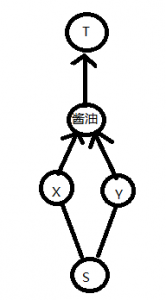
建一个这样的结构,x和y只有一个能使用这条边。最后统计流量看是否等于m。
#include <queue>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
int n,m,s,t;
int head[21000],to[101000],nxt[101000],f[101000],cnt=1;
inline void add(int x,int y,int z)
{
to[++cnt]=y; nxt[cnt]=head[x]; head[x]=cnt; f[cnt]=z;
to[++cnt]=x; nxt[cnt]=head[y]; head[y]=cnt; f[cnt]=0;
}
queue<int>q;
int dis[21000];
bool bfs()
{
memset(dis,-1,sizeof dis);
while(!q.empty()) q.pop();
q.push(s); dis[s]=0; int x;
while(!q.empty())
{
x=q.front(); q.pop();
for(int i=head[x];i;i=nxt[i])
if(f[i]>0&&dis[to[i]]<0)
{
dis[to[i]]=dis[x]+1;
if(to[i]==t) return true;
q.push(to[i]);
}
}
return false;
}
int dinic(int x,int flow)
{
if(x==t) return flow;
int xx,tmp=flow;
for(int i=head[x];i;i=nxt[i])
if(f[i]>0&&dis[to[i]]==dis[x]+1)
{
xx=dinic(to[i],min(f[i],tmp));
if(!xx) dis[to[i]]=-1;
f[i]-=xx; f[i^1]+=xx; tmp-=xx;
if(!tmp) break;
}
return flow-tmp;
}
bool check(int x)
{
for(int i=2;i<=cnt;i+=2)
f[i]+=f[i^1],f[i^1]=0;
for(int i=head[s];i;i=nxt[i]) f[i]=x;
int re=0;
while(bfs()) re+=dinic(s,1<<30);
return re==m;
}
int main()
{
scanf("%d%d",&n,&m); s=n+m+1,t=s+1;
int x,y;
for(int i=1;i<=n;i++) add(s,i,1);
for(int i=1;i<=m;i++)
{
add(n+i,t,1);
scanf("%d%d",&x,&y);
add(x,n+i,1);
add(y,n+i,1);
}
int l=0,r=10001,mid;
while(l<r)
{
mid=l+r>>1;
if(check(mid)) r=mid;
else l=mid+1;
}
printf("%d\n",r);
return 0;
}